CryptoDB
Topology-Hiding Communication from Minimal Assumptions.
| Authors: | |
|---|---|
| Download: | |
| Presentation: | Slides |
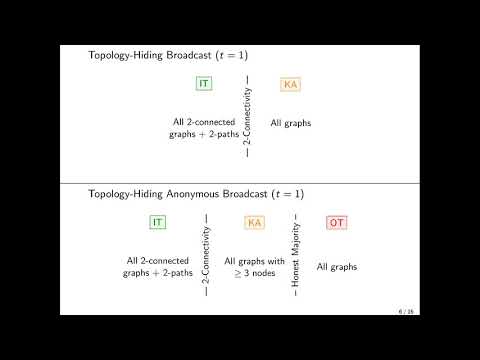
| Abstract: | Topology-hiding broadcast (THB) enables parties communicating over an incomplete network to broadcast messages while hiding the topology from within a given class of graphs. THB is a central tool underlying general topology-hiding secure computation (THC) (Moran et al. TCC’15). Although broadcast is a privacy-free task, it was recently shown that THB for certain graph classes necessitates computational assumptions, even in the semi-honest setting, and even given a single corrupted party. In this work we investigate the minimal assumptions required for topology-hiding communication—both Broadcast or Anonymous Broadcast (where the broadcaster’s identity is hidden). We develop new techniques that yield a variety of necessary and sufficient conditions for the feasibility of THB/THAB in different cryptographic settings: information theoretic, given existence of key agreement, and given existence of oblivious transfer. Our results show that feasibility can depend on various properties of the graph class, such as connectivity, and highlight the role of different properties of topology when kept hidden, including direction, distance, and/or distance-of-neighbors to the broadcaster. An interesting corollary of our results is a dichotomy for THC with a public number of at least three parties, secure against one corruption: information-theoretic feasibility if all graphs are 2-connected; necessity and sufficiency of key agreement otherwise. |
Video from TCC 2020
BibTeX
@article{tcc-2020-30640,
title={Topology-Hiding Communication from Minimal Assumptions},
booktitle={Theory of Cryptography},
publisher={Springer},
author={Marshall Ball and Elette Boyle and Ran Cohen and Lisa Kohl and Tal Malkin and Pierre Meyer and Tal Moran},
year=2020
}