CryptoDB
Horizontal racewalking using radical isogenies
| Authors: |
|
|---|---|
| Download: | |
| Presentation: | Slides |
| Conference: | ASIACRYPT 2022 |
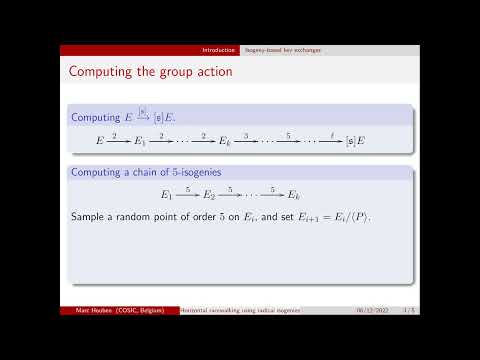
| Abstract: | We address three main open problems concerning the use of radical isogenies, as presented by Castryck, Decru and Vercauteren at Asiacrypt 2020, in the computation of long chains of isogenies of fixed, small degree between elliptic curves over finite fields. Firstly, we present an interpolation method for finding radical isogeny formulae in a given degree N, which by-passes the need for factoring division polynomials over large function fields. Using this method, we are able to push the range for which we have formulae at our disposal from N ≤ 13 to N ≤ 37. Secondly, using a combination of known techniques and ad-hoc manipulations, we derived optimized versions of these formulae for N ≤ 19, with some instances performing more than twice as fast as their counterparts from 2020. Thirdly, we solve the problem of understanding the correct choice of radical when walking along the surface between supersingular elliptic curves over Fp with p ≡ 7 mod 8; this is non-trivial for even N and was only settled for N = 4 by Onuki and Moriya at PKC 2022. We give a conjectural statement for all even N and prove it for N ≤ 14. The speed-ups obtained from these techniques are substantial: using 16-isogenies, the computation of long chains of 2-isogenies over 512-bit prime fields can be improved by a factor 3, and the previous implementation of CSIDH using radical isogenies can be sped up by about 12%. |
Video from ASIACRYPT 2022
BibTeX
@inproceedings{asiacrypt-2022-32650,
title={Horizontal racewalking using radical isogenies},
publisher={Springer-Verlag},
author={Wouter Castryck and Thomas Decru and Marc Houben and Frederik Vercauteren},
year=2022
}