CryptoDB
A Non-heuristic Approach to Time-space Tradeoffs and Optimizations for BKW
| Authors: |
|
|---|---|
| Download: | |
| Presentation: | Slides |
| Conference: | ASIACRYPT 2022 |
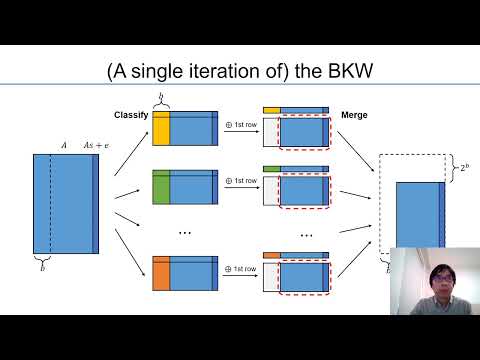
| Abstract: | Blum, Kalai and Wasserman (JACM 2003) gave the first sub-exponential algorithm to solve the Learning Parity with Noise (LPN) problem. In particular, consider the LPN problem with constant noise and dimension $n$. The BKW solves it with space complexity $2^{\frac{(1+\epsilon)n}{\log n}}$ and time/sample complexity $2^{\frac{(1+\epsilon)n}{\log n}}\cdot 2^{\Omega(n^{\frac{1}{1+\epsilon}})}$ for small constant $\epsilon\to 0^+$. We propose a variant of the BKW by tweaking Wagner's generalized birthday problem (Crypto 2002) and adapting the technique to a $c$-ary tree structure. In summary, our algorithm achieves the following: \begin{enumerate} \item {\bf (Time-space tradeoff).} We obtain the same time-space tradeoffs for LPN and LWE as those given by Esser et al. (Crypto 2018), but without resorting to any heuristics. For any $2\leq c\in\mathbb{N}$, our algorithm solves the LPN problem with time complexity $2^{\frac{\log c(1+\epsilon)n}{\log n}}\cdot 2^{\Omega(n^{\frac{1}{1+\epsilon}})}$ and space complexity $2^{\frac{\log c(1+\epsilon)n}{(c-1)\log n}}$, where one can use Grover's quantum algorithm or Dinur et al.'s dissection technique (Crypto 2012) to further accelerate/optimize the time complexity. \item {\bf (Time/sample optimization).} A further adjusted variant of our algorithm solves the LPN problem with sample, time and space complexities all kept at $2^{\frac{(1+\epsilon)n}{\log n}}$ for $\epsilon\to 0^+$, saving factor $2^{\Omega(n^{\frac{1}{1+\epsilon}})}$ in time/sample compared to the original BKW, and the variant of Devadas et al. (TCC 2017). \item {\bf (Sample reduction).} Our algorithm provides an alternative to Lyubashevsky's BKW variant (RANDOM 2005) for LPN with a restricted amount of samples. In particular, given $Q=n^{1+\epsilon}$ (resp., $Q=2^{n^{\epsilon}}$) samples, our algorithm saves a factor of $2^{\Omega(n)/(\log n)^{1-\kappa}}$ (resp., $2^{\Omega(n^{\kappa})}$) for constant $\kappa \to 1^-$ in running time while consuming roughly the same space, compared with Lyubashevsky's algorithm. \end{enumerate} In particular, the time/sample optimization benefits from a careful analysis of the error distribution among the correlated candidates, which was not studied by previous rigorous approaches such as the analysis of Minder and Sinclair (J.Cryptology 2012) or Devadas et al. (TCC 2017). |
Video from ASIACRYPT 2022
BibTeX
@inproceedings{asiacrypt-2022-32640,
title={A Non-heuristic Approach to Time-space Tradeoffs and Optimizations for BKW},
publisher={Springer-Verlag},
author={Hanlin Liu and Yu Yu},
year=2022
}