CryptoDB
Towards Tight Security Bounds for OMAC, XCBC and TMAC
| Authors: |
|
|---|---|
| Download: | |
| Presentation: | Slides |
| Conference: | ASIACRYPT 2022 |
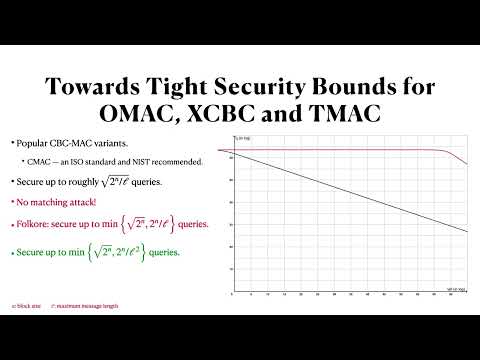
| Abstract: | OMAC --- a single-keyed variant of CBC-MAC by Iwata and Kurosawa --- is a widely used and standardized (NIST FIPS 800-38B, ISO/IEC 29167-10:2017) message authentication code (MAC) algorithm. The best security bound for OMAC is due to Nandi who proved that OMAC's pseudorandom function (PRF) advantage is upper bounded by $ O(q^2\ell/2^n) $, where $ q $, $ \ell $, and $ n $, denote the number of queries, maximum permissible query length (in terms of $ n $-bit blocks), and block size of the underlying block cipher, respectively. In contrast, there is no attack with matching lower bound. Indeed, the best known attack on OMAC is the folklore birthday attack achieving a lower bound of $ \Omega(q^2/2^n) $. In this work, we close this gap for a large range of message lengths. Specifically, we show that OMAC's PRF security is upper bounded by $ O(q^2/2^n + q\ell^2/2^n)$. In practical terms, this means that for a $ 128 $-bit block cipher, and message lengths up to $ 64 $ Gigabyte, OMAC can process up to $ 2^{64} $ messages before rekeying (same as the birthday bound). In comparison, the previous bound only allows $ 2^{48} $ messages. As a side-effect of our proof technique, we also derive similar tight security bounds for XCBC (by Black and Rogaway) and TMAC (by Kurosawa and Iwata). As a direct consequence of this work, we have established tight security bounds (in a wide range of $\ell$) for all the CBC-MAC variants, except for the original CBC-MAC. |
Video from ASIACRYPT 2022
BibTeX
@inproceedings{asiacrypt-2022-32619,
title={Towards Tight Security Bounds for OMAC, XCBC and TMAC},
publisher={Springer-Verlag},
author={Soumya Chattopadhyay and Ashwin Jha and Mridul Nandi},
year=2022
}