CryptoDB
Random Sources in Private Computation
| Authors: |
|
|---|---|
| Download: | |
| Conference: | ASIACRYPT 2022 |
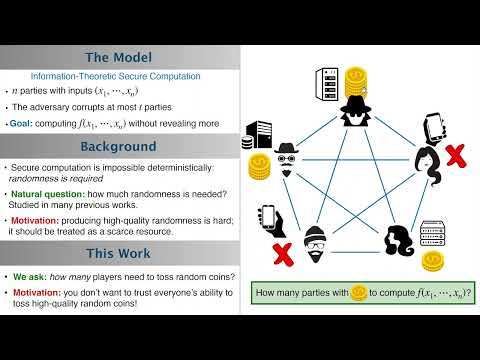
| Abstract: | We consider multi-party information-theoretic private computation. Such computation inherently requires the use of local randomness by the parties, and the question of minimizing the total number of random bits used for given private computations has received considerable attention in the literature.
In this work we are interested in another question: given a private computation, we ask how many of the players need to have access to a random source, and how many of them can be deterministic parties. We are further interested in the possible interplay between the number of random sources in the system and the total number of random bits necessary for the computation.
We give a number of results. We first show that, perhaps surprisingly, t players (rather than t+1) with access to a random source are sufficient for the information-theoretic t-private computation of any deterministic functionality over n players for any t |
Video from ASIACRYPT 2022
BibTeX
@inproceedings{asiacrypt-2022-32527,
title={Random Sources in Private Computation},
publisher={Springer-Verlag},
author={Geoffroy Couteau and Adi Rosén},
year=2022
}