CryptoDB
Polynomial IOPs for Linear Algebra Relations
| Authors: |
|
|---|---|
| Download: | |
| Presentation: | Slides |
| Conference: | PKC 2022 |
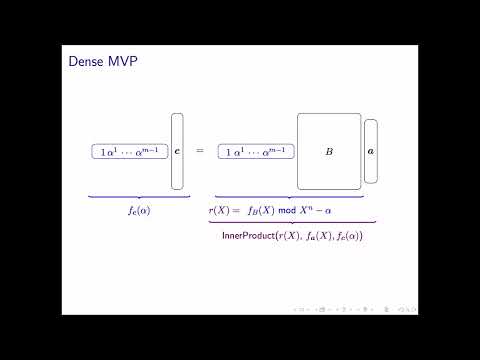
| Abstract: | This paper proposes new Polynomial IOPs for arithmetic circuits. They rely on the monomial coefficient basis to represent the matrices and vectors arising from the arithmetic constraint satisfaction system, and build on new protocols for establishing the correct computation of linear algebra relations such as matrix-vector products and Hadamard products. Our protocols give rise to concrete proof systems with succinct verification when compiled down with a cryptographic compiler whose role is abstracted away in this paper. Depending only on the compiler, the resulting SNARKs are either transparent or rely on a trusted setup. |
Video from PKC 2022
BibTeX
@inproceedings{pkc-2022-31815,
title={Polynomial IOPs for Linear Algebra Relations},
publisher={Springer-Verlag},
author={Alan Szepieniec and Yuncong Zhang},
year=2022
}