CryptoDB
Efficient Range Proofs with Transparent Setup from Bounded Integer Commitments
| Authors: |
|
|---|---|
| Download: |
|
| Presentation: | Slides |
| Conference: | EUROCRYPT 2021 |
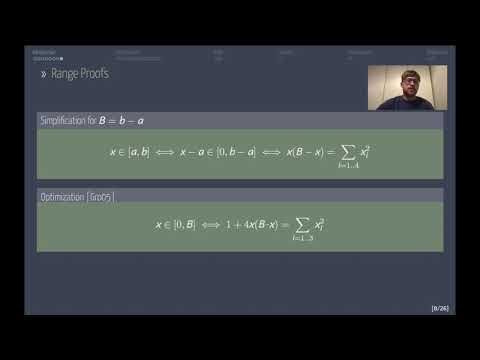
| Abstract: | We introduce a new approach for constructing range proofs. Our approach is modular, and leads to highly competitive range proofs under standard assumption, using less communication and (much) less computation than the state of the art methods, and without relying on a trusted setup. Our range proofs can be used as a drop-in replacement in a variety of protocols such as distributed ledgers, anonymous transaction systems, and many more, leading to significant reductions in communication and computation for these applications. At the heart of our result is a new method to transform any commitment over a finite field into a commitment scheme which allows to commit to and efficiently prove relations about bounded integers. Combining these new commitments with a classical approach for range proofs based on square decomposition, we obtain several new instantiations of a paradigm which was previously limited to RSA-based range proofs (with high communication and computation, and trusted setup). More specifically, we get: - Under the discrete logarithm assumption, we obtain the most compact and efficient range proof among all existing candidates (with or without trusted setup). Our proofs are 12% to 20% shorter than the state of the art Bulletproof (Bootle et al., CRYPTO'18) for standard choices of range size and security parameter, and are more efficient (both for the prover and the verifier) by more than an order of magnitude. - Under the LWE assumption, we obtain range proofs that improve over the state of the art in a batch setting when at least a few dozen range proofs are required. The amortized communication of our range proofs improves by up to two orders of magnitudes over the state of the art when the number of required range proofs grows. - Eventually, under standard class group assumptions, we obtain the first concretely efficient standard integer commitment scheme (without bounds on the size of the committed integer) which does not assume trusted setup. |
Video from EUROCRYPT 2021
BibTeX
@inproceedings{eurocrypt-2021-30859,
title={Efficient Range Proofs with Transparent Setup from Bounded Integer Commitments},
publisher={Springer-Verlag},
doi={10.1007/978-3-030-77883-5_9},
author={Michael Reichle and Michael Klooß and Geoffroy Couteau and Huang Lin},
year=2021
}