CryptoDB
FHE-Based Bootstrapping of Designated-Prover NIZK
| Authors: | |
|---|---|
| Download: | |
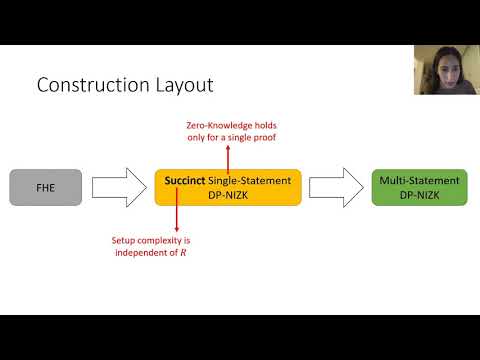
| Abstract: | We present a novel tree-based technique that can convert any designated-prover NIZK proof system (DP-NIZK) which maintains zero-knowledge only for single statement, into one that allows to prove an unlimited number of statements in ZK, while maintaining all parameters succinct. Our transformation requires leveled fully-homomorphic encryption. We note that single-statement DP-NIZK can be constructed from any one-way function. We also observe a two-way derivation between DP-NIZK and attribute-based signatures (ABS), and as a result derive now constructions of ABS and homomorphic signatures (HS). Our construction improves upon the prior construction of lattice-based DP-NIZK by Kim and Wu (Crypto 2018) since we only require leveled FHE as opposed to HS (which also translates to improved LWE parameters when instantiated). Alternatively, the recent construction of NIZK without preprocessing from either circular-secure FHE (Canetti et al., STOC 2019) or polynomial Learning with Errors (Peikert and Shiehian, Crypto 2019) could be used to obtain a similar final statement. Nevertheless, we note that our statement is formally incomparable to these works (since leveled FHE is not known to imply circular secure FHE or the hardness of LWE). We view this as evidence for the potential in our technique, which we hope can find additional applications in future works. |
Video from TCC 2020
BibTeX
@article{tcc-2020-30633,
title={FHE-Based Bootstrapping of Designated-Prover NIZK},
booktitle={Theory of Cryptography},
publisher={Springer},
author={Zvika Brakerski and Sanjam Garg and Rotem Tsabary},
year=2020
}