CryptoDB
Lossiness and Entropic Hardness for Ring-LWE
| Authors: | |
|---|---|
| Download: | |
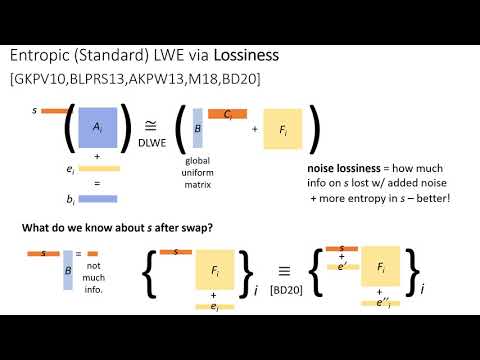
| Abstract: | The hardness of the Ring Learning with Errors problem (RLWE) is a central building block for efficiency-oriented lattice-based cryptography. Many applications use an ``entropic'' variant of the problem where the so-called ``secret'' is not distributed uniformly as prescribed but instead comes from some distribution with sufficient min-entropy. However, the hardness of the entropic variant has not been substantiated thus far. For standard LWE (not over rings) entropic results are known, using a ``lossiness approach'' but it was not known how to adapt this approach to the ring setting. In this work we present the first such results, where entropic security is established either under RLWE or under the Decisional Small Polynomial Ratio (DSPR) assumption which is a mild variant of the NTRU assumption. In the context of general entropic distributions, our results in the ring setting essentially match the known lower bounds (Bolboceanu et al., Asiacrypt 2019; Brakerski and Döttling, Eurocrypt 2020). |
Video from TCC 2020
BibTeX
@article{tcc-2020-30629,
title={Lossiness and Entropic Hardness for Ring-LWE},
booktitle={Theory of Cryptography},
publisher={Springer},
author={Zvika Brakerski and Nico Döttling},
year=2020
}