CryptoDB
Finding Hash Collisions with Quantum Computers by Using Differential Trails with Smaller Probability than Birthday Bound
| Authors: |
- Akinori Hosoyamada , NTT Secure Platform Laboratories / Nagoya University
- Yu Sasaki , NTT Secure Platform Laboratories
|
| Download: |
- DOI: 10.1007/978-3-030-45724-2_9
(login may be required)
- Search ePrint
- Search Google
|
|
Conference:
|
EUROCRYPT 2020
|
| Abstract: |
In this paper we spot light on dedicated quantum collision attacks on concrete hash functions, which has not received much attention so far.
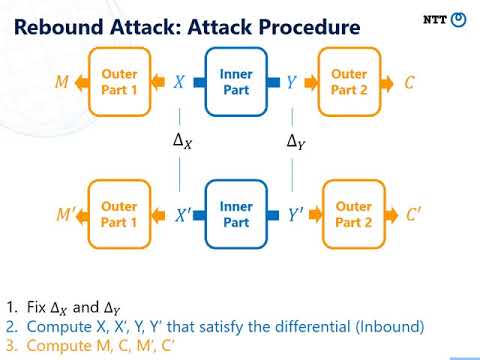
In the classical setting, the generic complexity to find collisions of an $n$-bit hash function is $O(2^{n/2})$, thus classical collision attacks based on differential cryptanalysis such as rebound attacks build differential trails with probability higher than $2^{-n/2}$.
By the same analogy, generic quantum algorithms such as the BHT algorithm find collisions with complexity $O(2^{n/3})$.
With quantum algorithms, a pair of messages satisfying a differential trail with probability $p$ can be generated with complexity $p^{-1/2}$.
Hence, in the quantum setting, some differential trails with probability up to $2^{-2n/3}$ that cannot be exploited in the classical setting may be exploited to mount a collision attack in the quantum setting.
In particular, the number of attacked rounds may increase.
In this paper, we attack two international hash function standards: AES-MMO and Whirlpool.
For AES-MMO, we present a $7$-round differential trail with probability $2^{-80}$ and use it to find collisions with a quantum version of the rebound attack,
while only $6$ rounds can be attacked in the classical setting.
For Whirlpool, we mount a collision attack based on a $6$-round differential trail from a classical rebound distinguisher with a complexity higher than the birthday bound. This improves the best classical attack on 5 rounds by 1.
We also show that those trails are optimal in our approach.
Our results have two important implications.
First, there seems to exist a common belief that classically secure hash functions will remain secure against quantum adversaries. Indeed, several second-round candidates in the NIST post-quantum competition use existing hash functions, say SHA-3, as quantum secure ones. Our results disprove this common belief.
Second, our observation suggests that differential trail search should not stop with probability $2^{-n/2}$ but should consider up to $2^{-2n/3}$.
Hence it deserves to revisit the previous differential trail search activities. |
Video from EUROCRYPT 2020
BibTeX
@inproceedings{eurocrypt-2020-30228,
title={Finding Hash Collisions with Quantum Computers by Using Differential Trails with Smaller Probability than Birthday Bound},
booktitle={39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, May 10–14, 2020, Proceedings},
series={Lecture Notes in Computer Science},
publisher={Springer},
keywords={symmetric key cryptgraphy;hash function;cryptanalysis;collision;quantum attack;AES-MMO;Whirlpool;rebound attack},
volume={12105},
doi={10.1007/978-3-030-45724-2_9},
author={Akinori Hosoyamada and Yu Sasaki},
year=2020
}