CryptoDB
Statistical Decoding 2.0: Reducing Decoding to LPN
| Authors: |
|
|---|---|
| Download: | |
| Presentation: | Slides |
| Conference: | ASIACRYPT 2022 |
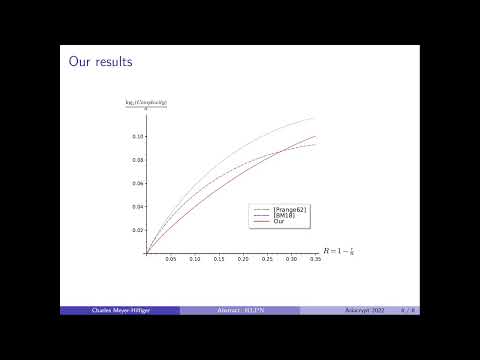
| Abstract: | The security of code-based cryptography relies primarily on the hardness of generic decoding with linear codes. The best generic decoding algorithms are all improvements of an old algorithm due to Prange: they are known under the name of information set decoders (ISD). A while ago, a generic decoding algorithm which does not belong to this family was proposed: statistical decoding. It is a randomized algorithm that requires the computation of a large set of parity-checks of moderate weight, and uses some kind of majority voting on these equations to recover the error. This algorithm was long forgotten because even the best variants of it performed poorly when compared to the simplest ISD algorithm. We revisit this old algorithm by using parity-check equations in a more general way. Here the parity-checks are used to get LPN samples with a secret which is part of the error and the LPN noise is related to the weight of the parity-checks we produce. The corresponding LPN problem is then solved by standard Fourier techniques. By properly choosing the method of producing these low weight equations and the size of the LPN problem, we are able to outperform in this way significantly information set decodings at code rates smaller than 0.3. It gives for the first time after 60 years, a better decoding algorithm for a significant range which does not belong to the ISD family. |
Video from ASIACRYPT 2022
BibTeX
@inproceedings{asiacrypt-2022-32574,
title={Statistical Decoding 2.0: Reducing Decoding to LPN},
publisher={Springer-Verlag},
author={Thomas Debris-Alazard and Jean-Pierre Tillich and Charles Meyer-Hilfiger and Kevin Carrier},
year=2022
}