CryptoDB
Computational Robust (Fuzzy) Extractors for CRS-dependent Sources with Minimal Min-entropy
| Authors: | |
|---|---|
| Download: | |
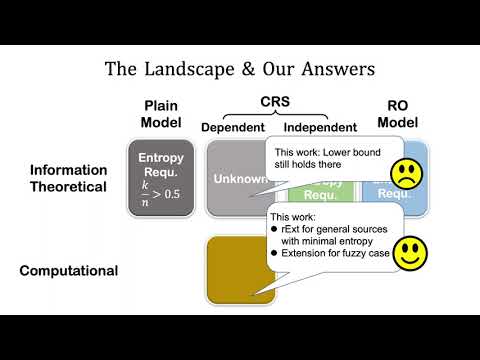
| Abstract: | Robust (fuzzy) extractors are very useful for, e.g., authenticated key exchange from a shared weak secret and remote biometric authentication against active adversaries. They enable two parties to extract the same uniform randomness with a ``helper'' string. More importantly, they have an authentication mechanism built in that tampering of the ``helper'' string will be detected. Unfortunately, as shown by Dodis and Wichs, in the information-theoretic setting, a robust extractor for an $(n,k)$-source requires $k>n/2$, which is in sharp contrast with randomness extractors which only require $k=\omega(\log n)$. Existing works either rely on random oracles or introduce CRS and work only for CRS-independent sources (even in the computational setting). In this work, we give a systematic study about robust (fuzzy) extractors for general CRS {\em dependent} sources. We show in the information-theoretic setting, the same entropy lower bound holds even in the CRS model; we then show we {\em can} have robust extractors in the computational setting for general CRS-dependent source that is only with minimal entropy. We further extend our construction to robust fuzzy extractors. Along the way, we propose a new primitive called $\kappa$-MAC, which is unforgeable with a weak key and hides all partial information about the key (both against auxiliary input); it may be of independent interests. |
Video from TCC 2021
BibTeX
@article{tcc-2021-31555,
title={Computational Robust (Fuzzy) Extractors for CRS-dependent Sources with Minimal Min-entropy},
booktitle={Theory of Cryptography;19th International Conference},
publisher={Springer},
doi={10.1007/978-3-030-90453-1_24},
author={Hanwen Feng and Qiang Tang},
year=2021
}